3. Trigonometry

c. Circle Definitions

Recall: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}\quad &\tan\theta&=\dfrac{y}{x}\quad &\sec\theta&=\dfrac{r}{x} \\[8pt] \cos\theta&=\dfrac{x}{r}\quad &\cot\theta&=\dfrac{x}{y}\quad &\csc\theta&=\dfrac{r}{y} \end{aligned}\]

2. Angles Bigger than \(90^\circ\)

When the angle is bigger than \(\dfrac{\pi}{2}\), we still use the same formulas for the trig functions, listed above.

Consider a circle centered at the origin and the ray at the angle \(\theta\) which passes through the point \((-12,35)\), find the radius of the circle and identify the six trig functions for the angle \(\theta\).

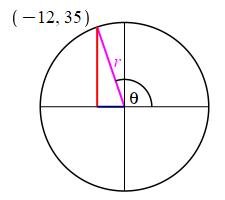
eg_12-35-37

Since the ray at the angle \(\theta\) passes through the point \((x,y)=(-12,35)\), the radius is \[ r=\sqrt{12^2+35^2}=\sqrt{144+1225}=\sqrt{1369}=37 \] So the trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}=\dfrac{35}{37}\quad &\tan\theta&=\dfrac{y}{x}=-\,\dfrac{35}{12}\quad &\sec\theta&=\dfrac{r}{x}=-\,\dfrac{37}{12} \\[8pt] \cos\theta&=\dfrac{x}{r}=-\,\dfrac{12}{37}\quad &\cot\theta&=\dfrac{x}{y}=-\,\dfrac{12}{35}\quad &\csc\theta&=\dfrac{r}{y}=\dfrac{37}{35} \end{aligned}\]

Consider a circle centered at the origin and the ray at the angle \(\theta\) which passes through the point \((-8,-15)\), find the radius of the circle and identify the six trig functions for the angle \(\theta\).

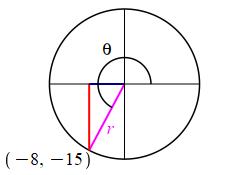
ex_8-15-17

\(r=17\)
\( \sin\theta=-\,\dfrac{15}{17}\quad \tan\theta=\dfrac{15}{8}\quad \sec\theta=-\,\dfrac{17}{8} \)

\( \cos\theta=-\,\dfrac{8}{17}\quad \cot\theta=\dfrac{8}{15}\quad \csc\theta=-\,\dfrac{17}{15} \)

Since the ray at the angle \(\theta\) passes through the point \((x,y)=(-8,-15)\), the radius is \[ r=\sqrt{8^2+15^2}=\sqrt{64+225}=\sqrt{289}=17 \] So the trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}=-\,\dfrac{15}{17}\quad &\tan\theta&=\dfrac{y}{x}=\dfrac{15}{8}\quad &\sec\theta&=\dfrac{r}{x}=-\,\dfrac{17}{8} \\[8pt] \cos\theta&=\dfrac{x}{r}=-\,\dfrac{8}{17}\quad &\cot\theta&=\dfrac{x}{y}=\dfrac{8}{15}\quad &\csc\theta&=\dfrac{r}{y}=-\,\dfrac{17}{15} \end{aligned}\]

Consider a circle centered at the origin and the ray at the angle \(\theta\) which passes through the point \((7,-24)\), find the radius of the circle and identify the six trig functions for the angle \(\theta\).

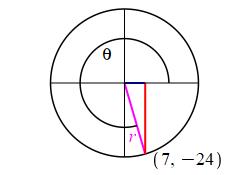
ex_7-24-25

\(r=25\)
\( \sin\theta=-\,\dfrac{24}{25}\quad\, \tan\theta=-\,\dfrac{24}{7}\quad \sec\theta=\dfrac{25}{7} \)

\( \cos\theta=\dfrac{7}{25}\qquad \cot\theta=-\,\dfrac{7}{24}\quad \csc\theta=-\,\dfrac{25}{24} \)

Since the ray at the angle \(\theta\) passes through the point \((x,y)=(7,-24)\), the radius is \[ r=\sqrt{7^2+24^2}=\sqrt{49+576}=\sqrt{625}=25 \] So the trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}=-\,\dfrac{24}{25}\quad &\tan\theta&=\dfrac{y}{x}=-\,\dfrac{24}{7}\quad &\sec\theta&=\dfrac{r}{x}=\dfrac{25}{7} \\[8pt] \cos\theta&=\dfrac{x}{r}=\dfrac{7}{25}\quad &\cot\theta&=\dfrac{x}{y}=-\,\dfrac{7}{24}\quad &\csc\theta&=\dfrac{r}{y}=-\,\dfrac{25}{24} \end{aligned}\]

© MYMathApps

Supported in part by NSF Grant #1123255